kategorie: matematyka
Witam Państwa,
W dzisiejszym artykule poznamy technikę obliczania całki nieoznaczonej z \(\frac{1}{x}\), sin(x), cos(x) (+ inne funkcje) oraz \(e^x\). Zapraszam! Nie będę się już tutaj raczej rozwodził dla każdego przykładu, nad tym dlaczego akurat całka z danej funkcji jest zdefiniowana tak a nie inaczej, ponieważ metodę stojącą za poprawnym całkowaniem już poznałeś/aś. Całka z danej funkcji -> jaka funkcja po zróżniczkowaniu da mi funkcję podcałkową? Przejdźmy zatem do rzeczy.
CAŁKI Z FUNKCJI TRYGONOMETRYCZNYCH
Całka nieoznaczona z funkcji: $$\int sin(x) dx = -cos(x) + C$$, gdzie C stanowi dowolnie dobraną stałą liczbową. Całka nieoznaczona z: $$\int cos(x) dx = sin(x) + C$$. Całka nieoznaczona z funkcji: $$\int sec^2(x) = tan(x) + C$$. Całka nieoznaczona z: $$\int csc^2(x) = -cot(x) + C$$. Całka nieoznaczona z: $$\int sec(x)tan(x) dx = sec(x) + C$$. Całka nieoznaczona z funkcji: $$\int csc(x)cot(x) dx = -csc(x) + C$$ Powyższe przykłady znajdziesz w zdjęciu pod tym materiałem 🙂
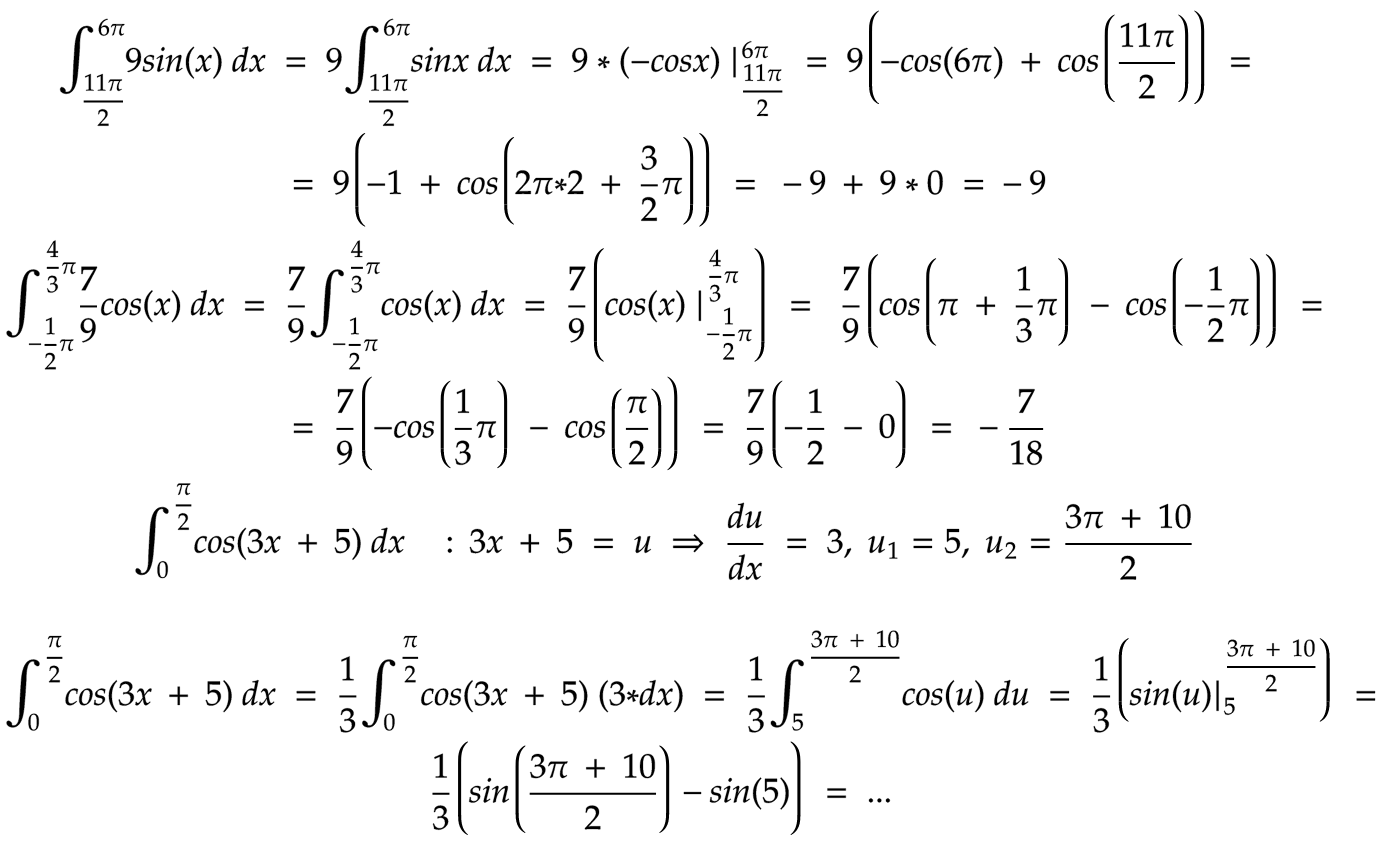
CAŁKA NIEOZNACZONA Z FUNKCJI E DO X
Teraz już krótka piłka. Całka nieoznaczona z funkcji: $$\int e^x$$ równa jest oczywiście $$e^x + C$$. Z czego jednak ten wzór się wywodzi? Z pewnością teraz w Twojej głowie pojawiła się myśl: "Ale o czym Ty w ogóle do mnie piszesz?! Przecież wystarczy spojrzeć do karty wzorów!" Istotnie! Jednak nie chcę byś tylko bez sensu zapamiętywał to co Ci podaję, ale też żebyś umiał/a to samemu sobie wyobrazić! Jak myślisz jaki będzie wynik scałkowania funkcji wykładniczej postaci a do potęgi x? Otóż jest to w istocie iloraz funkcji a do potęgi x oraz logarytmu naturalnego z a, tzn: $$\int a^x dx = \frac{a^x}{ln(a)}$$. Widzimy zatem, że jeżeli a = e to wówczas nasz mianownik będzie dawał w rezultacie wynik 1, co ostatecznie doprowadzi nas do wyniku znajdującego się liczniku postaci: \(e^x + C\). Nie martw się jeśli tego nie zrozumiałeś. Spróbuj wziąć sobie czystą kartkę papieru i rozpisać to o czym przed chwilką mówiłem 🙂 Na pewno wtedy zrozumiesz!
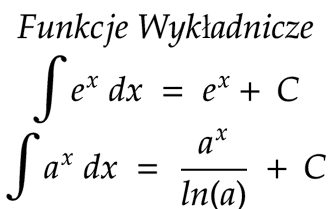
CAŁKA Z 1 / X
Ostatnią całką jaką się dzisiaj zajmiemy będzie całka z funkcji \(\frac{1}{x}\). W istocie wynikiem będzie tutaj ln|x| + C. Dowód tego faktu jest troszkę skomplikowany i na tym poziomie na jakim jesteśmy zupełnie niepotrzebny. Daję Ci tylko to co ułatwi Ci posługiwanie się całkami!
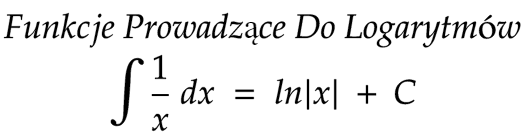
BONUS
Teraz jeszcze chciałbym Ci podarować pewien bonus! Nie jest to jednak dla Ciebie obowiązkowe, gdyż nie będziemy robić z tego przykładów (z faktu iż jest to po prostu bardzo czasochłonne). Jednak mimo to zachęcam Cię do zrobienia parę przykładów które z tego się pojawią w jednym z następnych materiałów (Oczywiście to nie będzie tak, że dam Ci całki i na żywioł będziesz je próbował rozwiązywać! Oczywiście że nie! Byłoby to bardzo nierozsądne z mojej strony 🙂 Umówmy się tak: rozwiąże po 3 przykłady z każdego tematu jaki przedstawiam (i będzie to najcięższe jakie spotkasz), a później Ty (jeśli tylko będziesz miał ochotę, bo też nic na siłę) rozwiążesz według możliwości 2 kolejne przykłady! Nie martw się będą naprawdę proste! Ale to dopiero za jakieś 2 artykuły. Muszę Ci jeszcze parę rzeczy pokazać!) A zatem bonus:
$$\int \frac{1}{\sqrt{a^2 - x^2}} dx = arcsin(\frac{x}{a}) + C$$
$$\int \frac{1}{a^2 + x^2} dx = \frac{1}{a} * arctan(\frac{x}{a}) + C$$
Jak widzisz nie są to łatwe wzory i zapewniam -> nie są one także łatwe w użytkowaniu i wymagają treningu! Dziękuję za przeczytanie!
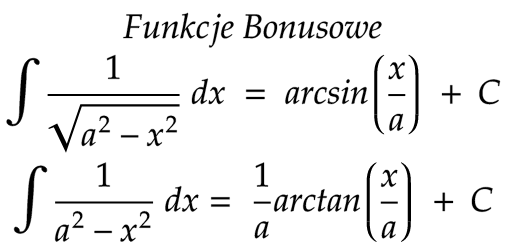
Pozdro 🙂
Czytaj dalej

