kategorie: matematyka
Witam Państwa,
Mamy za sobą już tak naprawdę większość informacji potrzebnych do obliczenia dowolnego pola pod krzywą określoną dowolnym wzorem na dowolnym przedziale. Poznaliśmy metody aproksymacji pola pod wykresem. Poznaliśmy także definicję całki oznaczonej oraz podstawowe twierdzenie rachunku całkowego. Pokażę Ci dziś jak łatwo możesz obliczyć pole pod wykresem dowolnej funkcji potęgowej, używając oczywiście pojęcia całki.
OBLICZANIE CAŁKI NIEOZNACZONEJ Z FUNKCJI POTĘGOWEJ
Powiedzmy zatem, że mamy daną całkę nieoznaczoną z funkcji x do potęgi n, gdzie n jest różne od -1. Tzn.: $$\int x^n dx$$ Ponieważ schemat, który Ci przedstawię nie działa dla tej potęgi (-1). Wracając... Chcąc obliczyć taką całkę powinniśmy oczywiście zwiększyć wykładnik x o 1, zatem będziemy mieć: $$x^n+1$$. Następnie całość podzielić przez (n + 1). Teraz pojawia się pytanie dlaczego? Przypatrz się dokładnie (najlepiej żebyś sobie to zapisał/a). Jeżeli zróżniczkujesz funkcję x do potęgi (n + 1) przez (n + 1), wykładnik pójdzie Ci przed x i sam wykładnik zostanie zmniejszony o jeden. Popatrz: $$\frac{(n + 1)*x^{n+1-1}}{(n + 1)}$$ W rezultacie (n + 1) w liczniku skróci się z (n + 1) w mianowniku i zostanie nam sama funkcja: $$x^n$$, czyli nasza wyjściowa funkcja, którą całkowaliśmy. Zatem widzimy, że możemy w ten właśnie sposób obliczyć dowolną całkę z funkcji potęgowej.
WŁASNOŚCI CAŁEK
Teraz zapoznajmy się z własnościami całek by z wiedzą jaką już posiadamy móc obliczyć całkę z dowolnego wielomianu stopnia n różnego od -1. Powiedzmy, że mamy całkę nieoznaczoną z sumy dwóch funkcji: f(x) oraz g(x). Wówczas wynikiem będzie suma całki f(x) oraz g(x). Nie martw się jeżeli nic nie zrozumiałeś z tego co właśnie napisałem. Poniżej znajdzie się fotka obrazująca wszystkie najważniejsze (nam w szczególności potrzebne) własności całek. Kolejna warta zapamiętania własność całki jest taka, że jeżeli mamy pod naszą całką pewną stałą (możemy ją oznaczyć jako k), to wówczas stałą tą możemy wyciągnąć przed całkę (fotka pod materiałem). Kolejna własność jest taka, że możemy sobie zamieniać dowolnie przedział całkowania (mam na myśli, że możesz sobie zamienić miejscami dolny przedział z górnym), pamiętając tylko o dopisaniu do wyjściowej funkcji znaku minus. Dalej... jeżeli całkujesz na przedziale od a do a, dla a należącego do zbioru liczb rzeczywistych, wówczas pole określone taką całką wyniesie 0. Na końcu "cream de la cream". Coś co pozwoli nam obliczać "chore dziadostwo (wiem co mówię)" czyli całki oznaczone z funkcji trygonometrycznych i cyklometrycznych na przedziałach (oczywiście na końcu kursu też dam Ci parę przykładów z całką na przedziale, ze zwykłego wielomianu). To tyle, dzięki za przeczytanie tego artykułu!
Pozdro 🙂
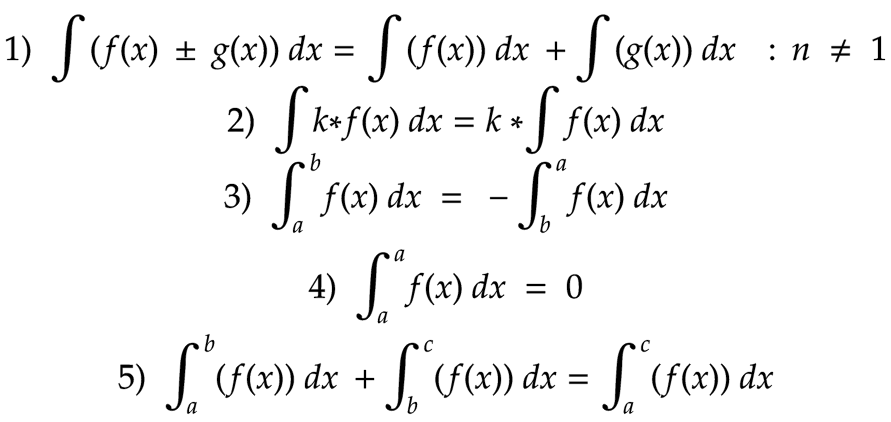
Czytaj dalej

